Gray Codes and Their Uses in Digital Design

What are Gray Codes?

Gray code is a binary code in which only one bit changes between adjacent values. This property makes it useful in a variety of applications where reliable and accurate data transmission is required.

One common application of Gray code is in rotary encoders, which are devices used to convert the angular position of a shaft into an electrical signal. Rotary encoders typically use a binary code to represent the shaft position, but the changing position of the shaft can create glitches or noise in the code. By using Gray code instead of binary code, only one bit changes at a time as the shaft rotates, minimizing the potential for errors or false readings.

Another practical usage of Gray code is in digital-to-analog converters (DACs), which convert digital signals into analog voltages or currents. DACs often use resistor networks to generate the analog output, and Gray code can be used to ensure that only one resistor changes value between adjacent digital codes. This can reduce the potential for glitches or non-monotonic behavior in the analog output.

Gray code can also be useful in signal processing applications, where it can be used to generate waveforms with minimal harmonic distortion. By ensuring that only one bit changes at a time, Gray code can produce smooth and continuous transitions between adjacent values, reducing the potential for distortion or artifacts in the waveform.

Overall, Gray code is a useful encoding scheme in applications where accuracy, reliability, and minimal distortion are important factors. Its unique properties make it a valuable tool in a variety of fields, including electrical engineering, computer science, and signal processing.

💡If you have worked with Karnaugh Maps or K-Maps, you have already seen a practical use of Gray Codes.

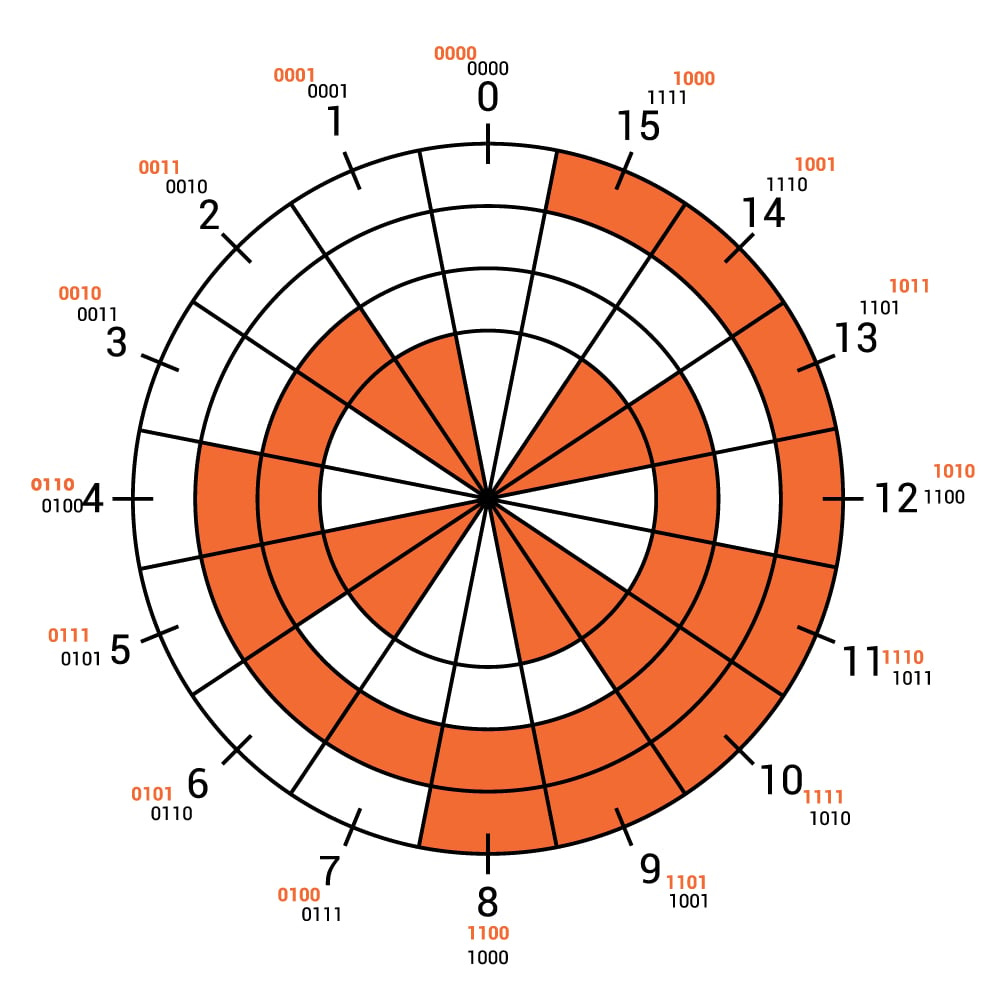
During one of my interviews, I was asked to generate 4-bit Gray codes for binary numbers 0 through 15. Here’s a neat trick using a K-map to do that! ⚡⚡
We know that each cell in a K-map differs from its adjacent cell by a single bit. So, if you start at the top-left corner and draw a zig-zag line across the K-map, you’ll end up with a sequence of Gray codes.

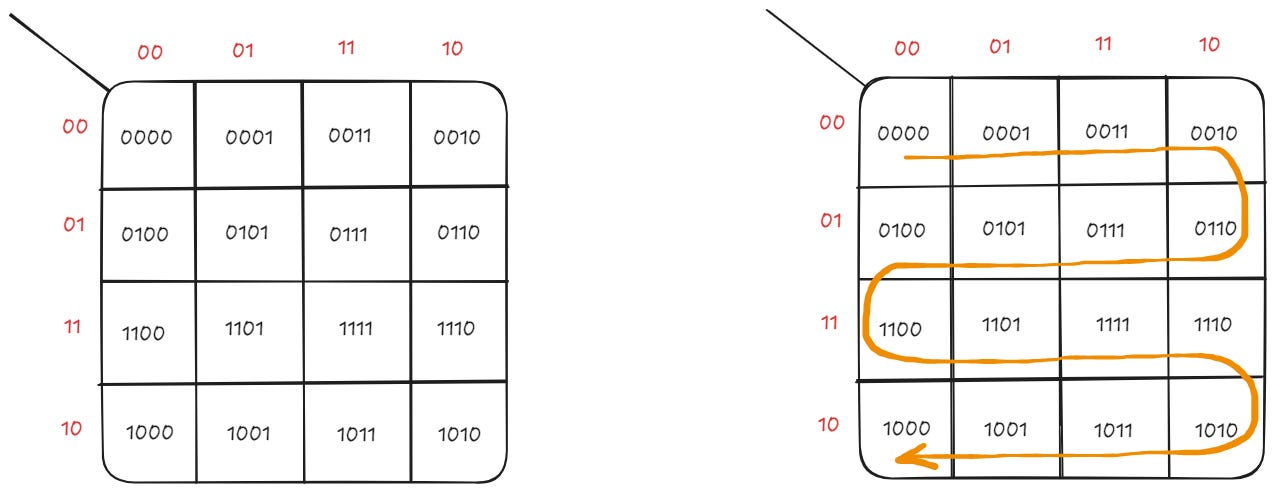
Generating a Gray Code Equivalent for Binary Code

Generating Gray codes from binary is straightforward and involves a simple bitwise operation. Here’s the technique:

1. Retain the Most Significant Bit (MSB): The MSB of the Gray code is the same as the MSB of the binary code.
2. XOR Operation: For each subsequent bit, perform an XOR operation between the current bit and the previous bit of the binary number.

Example: Convert Binary 1011 to Gray Code

1. Binary: 1011
2. Gray Code:
   • MSB: 1 (same as binary)
   • Next bit: 0 XOR 1 = 1
   • Next bit: 1 XOR 0 = 1
   • Next bit: 1 XOR 1 = 0

So, the Gray code equivalent of binary 1011 is 1110.